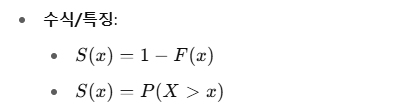통계

• 통계
• 확률 변수 : 무작위 실험의 결과에 의해 값이 결정되는 변수
  • 이산형 확률 변수 : 셀 수 있는 값을 가진다.
  • 연속형 확률 변수 : 특정 범위 내의 모든 실수 값을 가질 수 있다.
• 확률 분포 : 확률 변수가 특정 값 또는 값의 범위에 속할 확률을 나탄는 함수 또는 규칙
• 정규 분포가 제일 대표적인 예 

주요 연속 확률 분포

 

• 정규 분포
  • 정의 :
  • 특징 :  종 모양의 대칭적인 분포 / 평균 = 중앙값 = 최빈값 / Z ~ N(0, 1)로 평균이 0이고, 표준편차가 1인 정규 분포
  • 활용 : 많은 통계적 방법론의 기초 가정, 금융 자산의 수익률 모델링 및 측정 오차에서 활용

 

• t - 분포
  • 정의 : 정규 분포롸 유사한 종 모양이지만, 꼬리가 더 두꺼움
  • 특징 : 극단적인 값이 나타날 확률이 정규분포보다 높다 
  • 활용 : 소표본에서의 평균 검정 및 추정

• 카이제곱 분포
  
  • 정의 : 여러개의 서로 독립적인 표준정규 분포를 따르는 확률변수들을 각각 제곱한 다음 모두 더해서 얻어지는 분포
  • 특징 : 오른쪽으로 긴 꼬리를 가지는 비대칭 분포 / 자유도가 커질수록 대칭서에 가까워짐
  • 활용 : 분산 추정 및 검정, 적합도 검정, 독립성 검정 등에 활용

 

• 지수 분포
  • 정의 : 어떤 사건이 처음 발생하기까지 걸리는 대기 시간
  • 특징 :
  • 활용 : 부품의 수명 예측, 고객이 서비스 받기까지 기다리는 시간

특징	이항분포	포아송분포
정의	서로 독립적인 베르누이 시행을 n번 반복했을 때 나타나는 성공 횟수 k의 확률 분포	단위 시간, 단위 공간, 또는 단위 부피 등 특정 구간 내에서 어떤 사건이 발생하는 평균 횟수를 알 때, 실제 그 사건이 k번 발생할 확률 분포
모수	시향 횟수 n, 성공 확률 p	평균 발생 횟수
확률변수	0, 1, ..., n (정수)	0, 1, 2 ,...(정수)
평균	np	lambda
분산	np(1-p)	lambda
적용예시	제품 불량품 수, 여론조사 특정 후보 지지자 수	단위 시간 내 교차로 차량 수, 서버 요청 수

 

• PMF( Probability Mass Function )
  • 이산 확률 변수 XXX에 대해, 변수가 특정 값 xix_ixi​를 가질 확률 P(X=xi)P(X = x_i)P(X=xi​)를 나타낸다
  • 모든 가능한 xix_ixi​에 대한 PMF 값의 합은 1이다.  ∑iP(X=xi)=1\sum_i P(X = x_i) = 1i∑​P(X=xi​)=1
  • 이산 확률 변수에만 적용
• PDF( Probability Density Function)
  • 연속 확률 변수 XXX에 대해, 변수가 특정 구간 [a,b][a, b][a,b]에 속할 확률 P(a≤X≤b)P(a \leq X \leq b)P(a≤X≤b)는 PDF f(x)f(x)f(x)를 해당 구간에서 적분한 값  ∫ab​f(x)dx으로 계산
  • 연속 확률 변수에서 특정 한 지점에서의 확률은 0입니다 (P(X=x)=0P(X = x) = 0P(X=x)=0).
  • 연속 확률 변수에만 적용

• CDF(Cumulative Distribution Function)
  • 확률 변수 XXX가 특정 값 xxx보다 작거나 같을 확률을 나타낸다
  • 모든 확률 변수에 적용

• SF( Survival Function )
  • 확률 변수 XXX가 특정 값 xxx보다 클 확률을 나타낸다.  S(x)=P(X>x)S(x) = P(X > x)S(x)=P(X>x)
  • 모든 확률 변수에 적용 (생존 분석, 신뢰성 공학 등에서 사용)